Fotos de lugares donde se aplica este número

En primer lugar tenemos la Mezquita de Córdoba. En segundo lugar tenemos la Bóveda cordobesa. Por último tenemos la Fachada de el Convento de Capuchinos en Córdoba.

Aquí tenemos la Puerta de Alhaken II de la Mezquita de Córdoba.

Aplicación práctica del número cordobés

Consideremos la circunferencia de radio R. Si trazamos la bisectriz del primer cuadrante, el segmento NP= X es el lado del octógono regular inscrito en dicha circunferencia. Aplicando el teorema de Pitágoras al triángulo NOM resulta que:

(MN)2 = R2 + R2

por lo que:

Por simetría OP'= MN/2 (ya que NP'=MN/2 y OP'=P'N)

Como QNP es recto, aplicando el teorema del cateto resulta:

X /QP = P'P/ X
de donde:

X2 = QP. P'P = 2R (OP - OP')
es decir:
De esta expresión deducimos (considerando la circunferencia de radio unidad, radio R = 1) que:

Determinación sobre la recta real del número cordobés C:

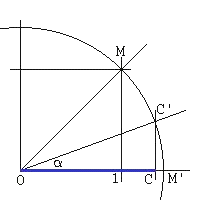
Consideramos el segmento unidad y trazamos una circunferencia de radio (2)1/2 La bisectriz del ángulo MOM' corta a dicha circunferencia en C'. Proyectando sobre la recta real obtenemos C. En efecto
En el triángulo OCC'
Observa que
es la expresión trigonométrica del número cordobés.

Teoría del número cordobés

El número cordobés es la relación existente entre el radio de la circunferencia circunscrita al octógono regular y el lado de este.

Este número se utiliza en diversos trabajos de investigación (arquitectura, pintura, etc.), aparece un rectángulo que no está en la proporción áurea*.

La fórmula para averiguar el número cordobés, es:






Este cociente es c= 1.30656... y este número se conoce como número cordobés


* Es la relación existente entre el decágono regular y el radio de la circunferencia circunscrita del mismo.

Algunos ejemplos en los que se demuestra que se aplica el número cordobés, son:

- La bóveda cordobesa
- La mezquita-catedral de Córdoba

Según los trabajos del alemán Fechner, este cociente se establece en multitud de obras pictóricas.

El arquitecto Rafael de la Hoz Arderius, considerando las últimas mediciones obtenidas del Papiro Rhind, entre las diagonales de un rectángulo de dicha proporción encaja perfectamente la Gran Pirámide.