Aplicación práctica del número cordobés

Consideremos la circunferencia de radio R. Si trazamos la bisectriz del primer cuadrante, el segmento NP= X es el lado del octógono regular inscrito en dicha circunferencia. Aplicando el teorema de Pitágoras al triángulo NOM resulta que:

(MN)2 = R2 + R2

por lo que:

Por simetría OP'= MN/2 (ya que NP'=MN/2 y OP'=P'N)

Como QNP es recto, aplicando el teorema del cateto resulta:

X /QP = P'P/ X
de donde:

X2 = QP. P'P = 2R (OP - OP')
es decir:
De esta expresión deducimos (considerando la circunferencia de radio unidad, radio R = 1) que:

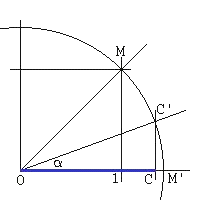
Determinación sobre la recta real del número cordobés C:

Consideramos el segmento unidad y trazamos una circunferencia de radio (2)1/2 La bisectriz del ángulo MOM' corta a dicha circunferencia en C'. Proyectando sobre la recta real obtenemos C. En efecto
En el triángulo OCC'
Observa que
es la expresión trigonométrica del número cordobés.